Apr 15, 20216 min read

Why Fibonacci Numbers Show Up in Plants

Updated: Apr 27, 2021

By Jenny Lam

sunflower — Image Credit: Flickr @ Sue Reynolds

Nature’s Spirals

Spirals, curves that originate from a point and circle around and around as they get bigger, are everywhere in nature. From hurricanes, to shells, to plants, these mesmerizing curves have expanded their presence to every corner of biology. Plants, in particular, are especially interesting to examine, as the petals, stigmata (middle parts of flowers), cones, and leaves around a stem can all display spiral-like patterns.

It’s easy to simply look and admire the intricacy of these plants, but what if we actually counted the spirals?

For the sunflower picture from above, we see 55 spirals going clockwise and 34 spirals going counterclockwise.

Modified: Image Credit: Flickr @ Sue Reynolds

At first, these numbers may seem arbitrary but if we take a look at many more plants, you’ll see the same seemingly random numbers pop up over and over again: 13, 34, 21, 55, 8, and 5.

Is there some biological number rule going on here? What’s really happening?

The Fibonacci Sequence

These numbers might look familiar to those who know of the Fibonacci sequence: a sequence of numbers where each number is the sum of the 2 numbers behind it. Starting with 0, the sequence looks like this:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc…

2 is the sum of 1 and 1, 13 is the sum of 5 and 8, and so on. More specifically, it’s defined by the equation Fn=Fn-1+Fn-2, with F0 being 0 and F1 being 1. The Fibonacci numbers can be seen in the famous “golden rectangle” or “golden spiral”.

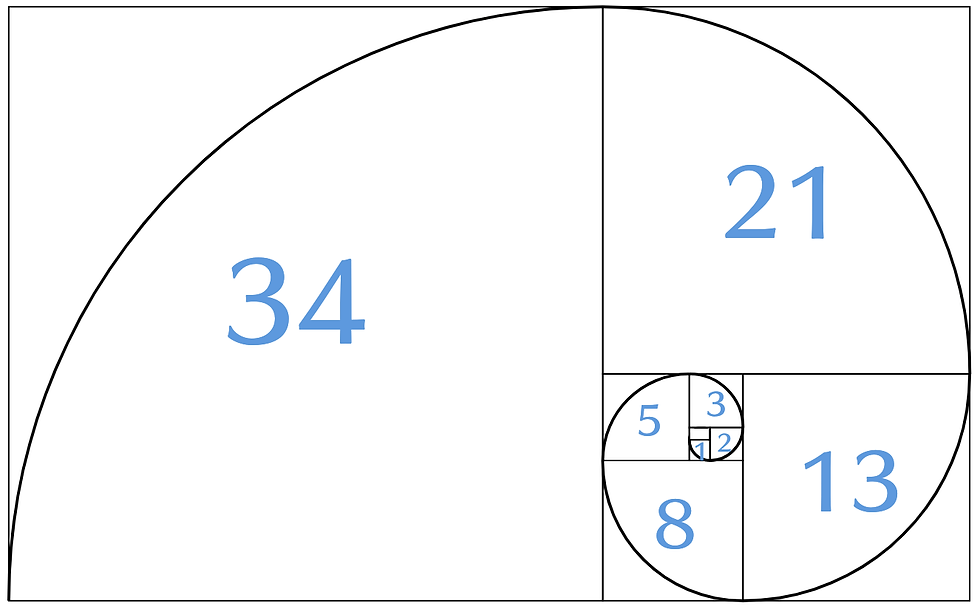
Image Credit: Wikimedia Commons @ Raymondprucher

The numbers in each box represent the length of the sides of each square, and each square’s length is made up of the lengths of the last two squares, just like those Fibonacci numbers. Interestingly, watch what happens if we find the ratio between two successive Fibonacci numbers:

3/2=1.5

5/3=1.6

8/5=1.6

13/8=1.625

21/13=1.615384

34/21=1.619047

As we pick bigger and bigger numbers in the sequence, the ratio of the two numbers will approach an irrational number--perhaps one of the most irrational among irrational numbers: 1.61803…, also known as the golden ratio or ϕ (phi).

Filling Up Space: Demonstrating Nature’s Efficiency

Now we know that numbers of the Fibonacci sequence just happen to show up in plants. What’s the connection?

plant; fibonacci sequence — Image Credit: Flickr @ Dennis Hill

The first thing we learn about plants is that they need light and water to grow, with light coming from the sun and the water coming from rain. The second thing we learn about them is that the energy from the sun and the water is used in photosynthesis to be converted into organic compounds for growth. Photosynthesis takes place in the leaves of a plant, so more leaf exposure to sunlight translates to more photosynthesis taking place. Additionally, more leaf exposure will also allow the plant to catch more rainwater, as well. Leaves don’t spout out of a stem sporadically at random locations; rather, they grow in spirals around the stem. Similarly, the seeds in the middle of many flowers also grow out in spirals, as well as the petals of daisies and sunflowers. Like the leaves on a stem, filling up space to maximize petal surface area is also optimal for survival and reproduction, as it would garner more attention to attract potential pollinators.

Since leaves grow in a spiral pattern, how far apart should each leaf be in order to fill up the most space?

If the leaves were 120° apart, or 1/3 of a full turn, we would get a plant that looks something like this:

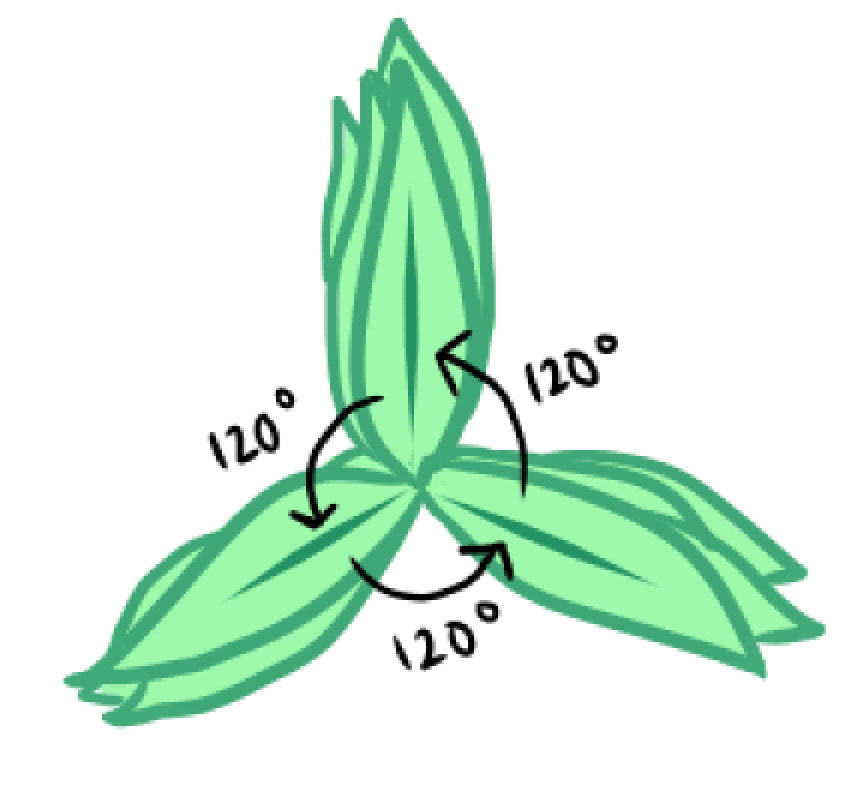
This leaf arrangement doesn’t fill up a lot of space, and the leaves below the top 3 leaves would barely get any exposure at all. If we try out some more angles, we can see that the leaves would just end up overlapping each other completely after 1 full turn has been completed. For the example above, this occurred after 3 leaves, as leaves are being grown 1/3 of a full turn apart.

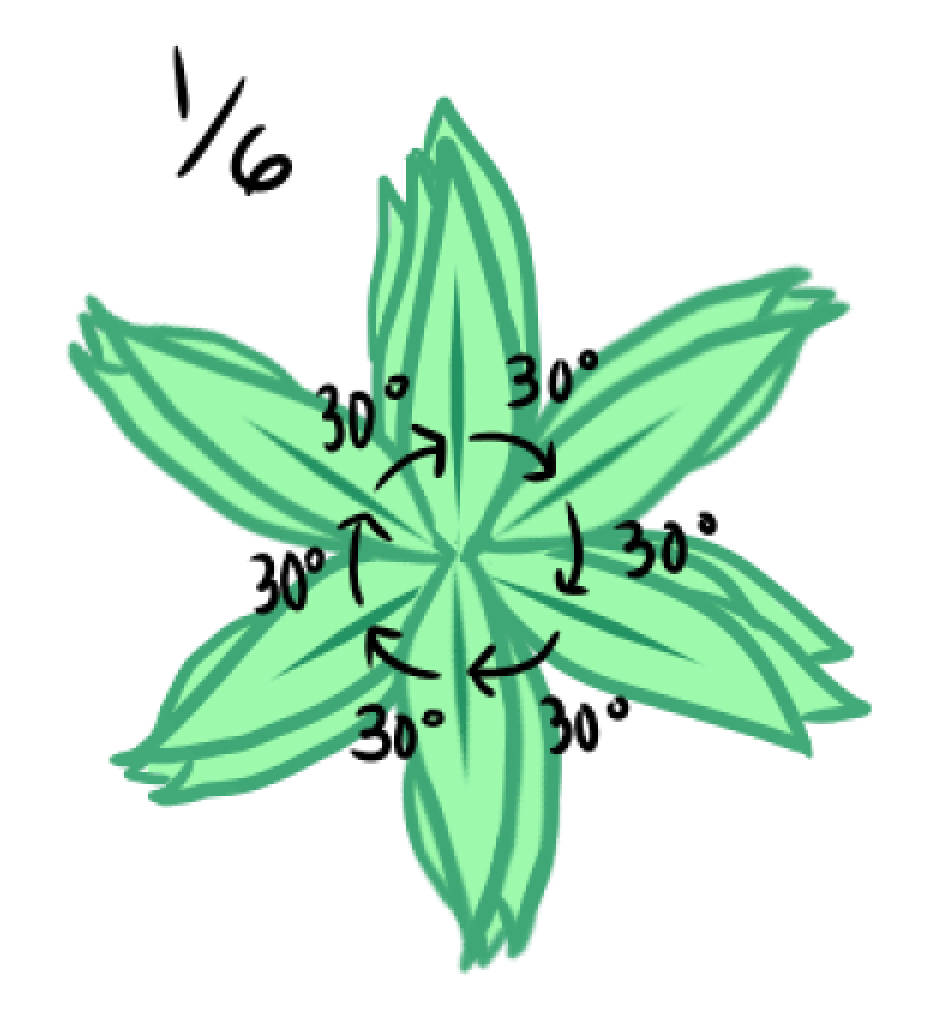
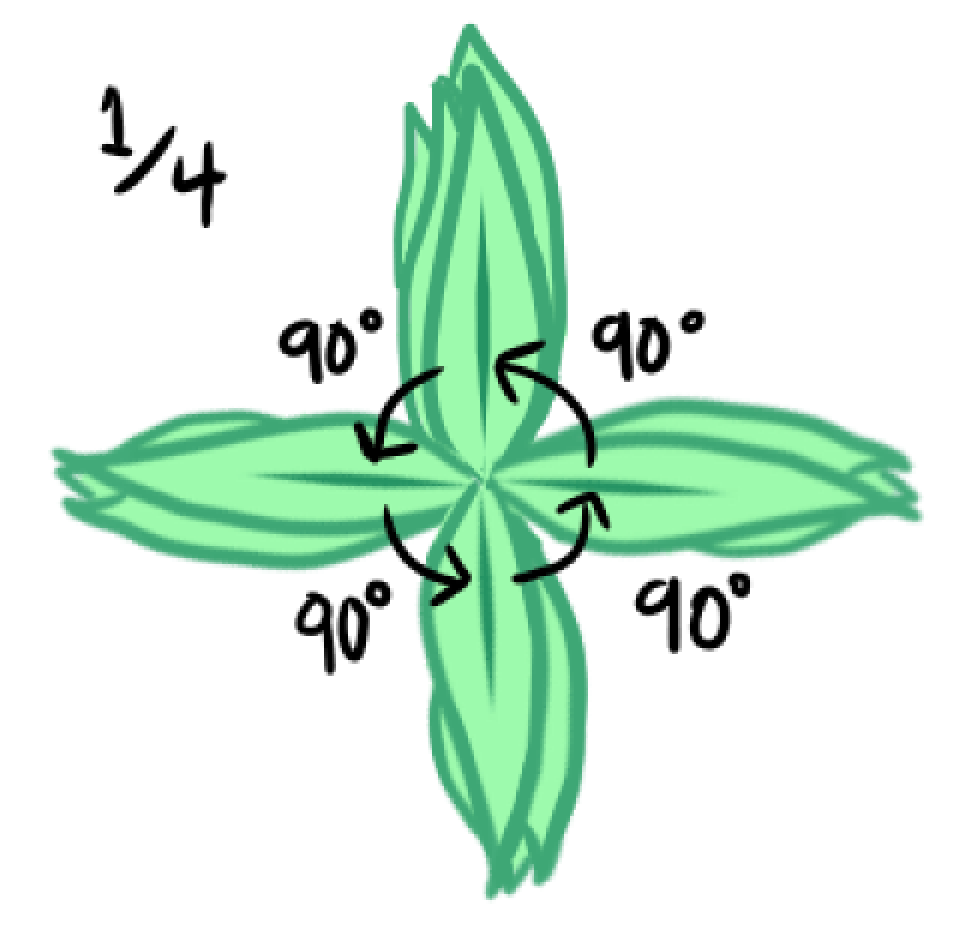
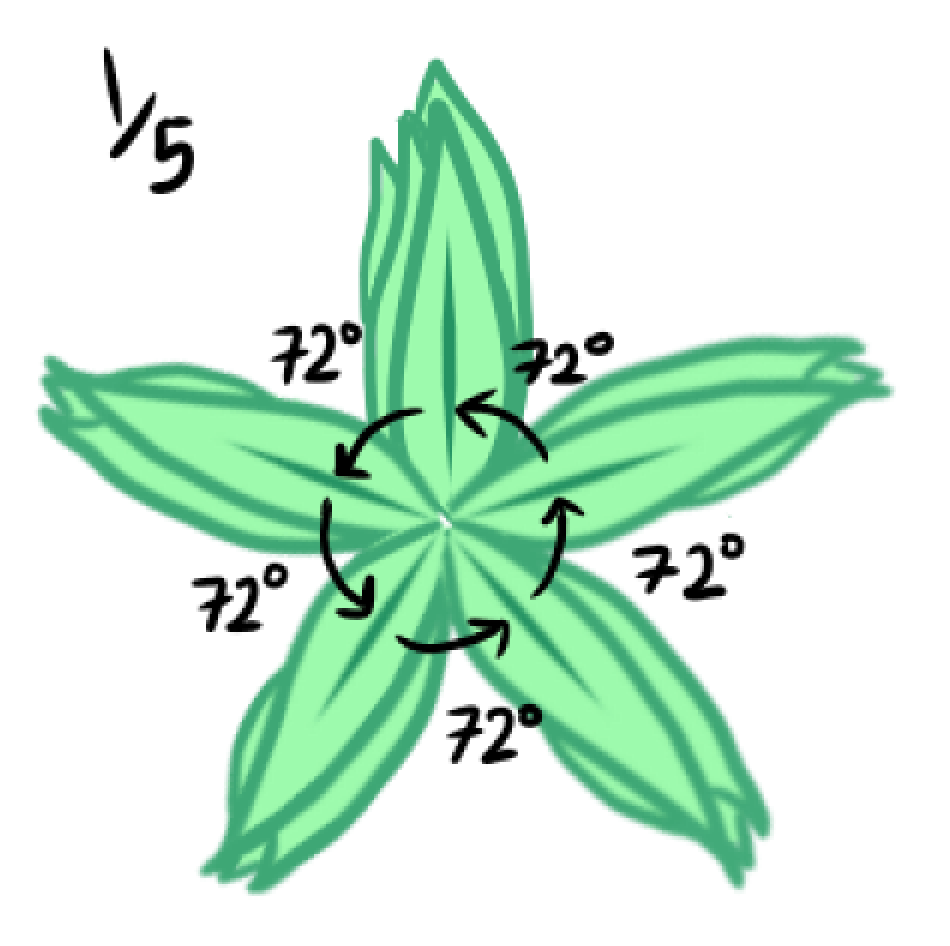
These leaf arrangements do fill up more space compared to the first one, but there still remains some extra space that can be filled up more. Like the first arrangement, the leaves will start to get covered up by other leaves after the first full turn. To get a plant where the leaves won’t get completely covered up, each leaf shouldn’t be 1/3, 1/10, or 1 over a whole number of a circle apart—or else after a full turn, the leaves would just overlap each other.

Perhaps, 1 over an irrational number might do the trick. More specifically, it should be a number that can’t be well approximated by a simple fraction. This is where the golden ratio, ϕ (1.618...), comes into play. A plant where its leaves (or petals) are 1/ϕ of a circle apart, or about 137.5° (the golden angle!), will never have its leaves completely overlap each other, therefore filling up the most space.

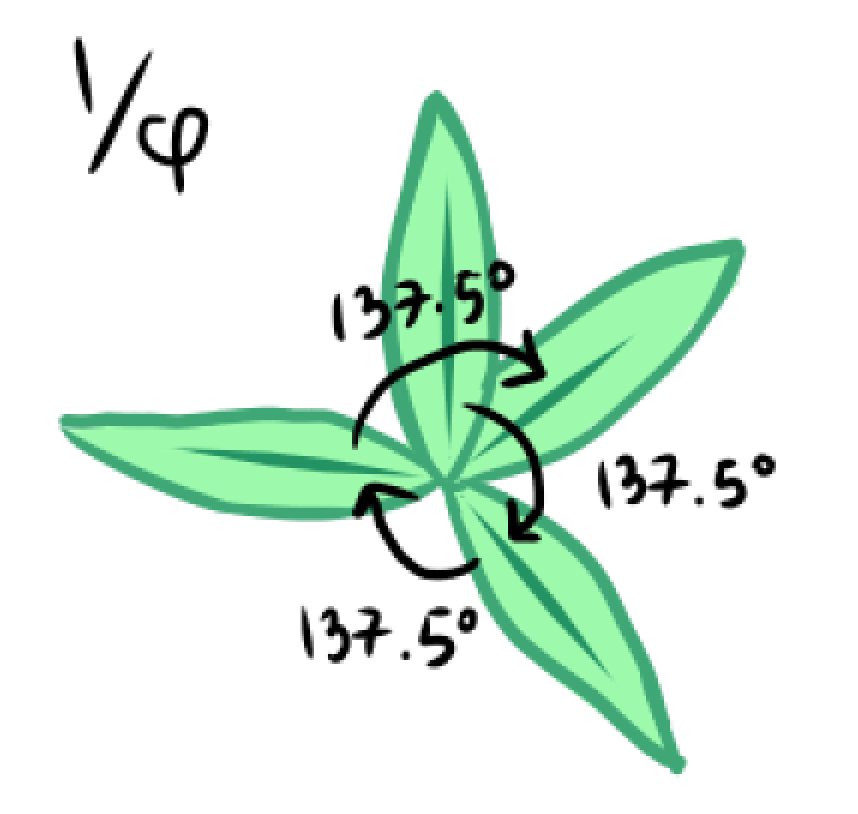
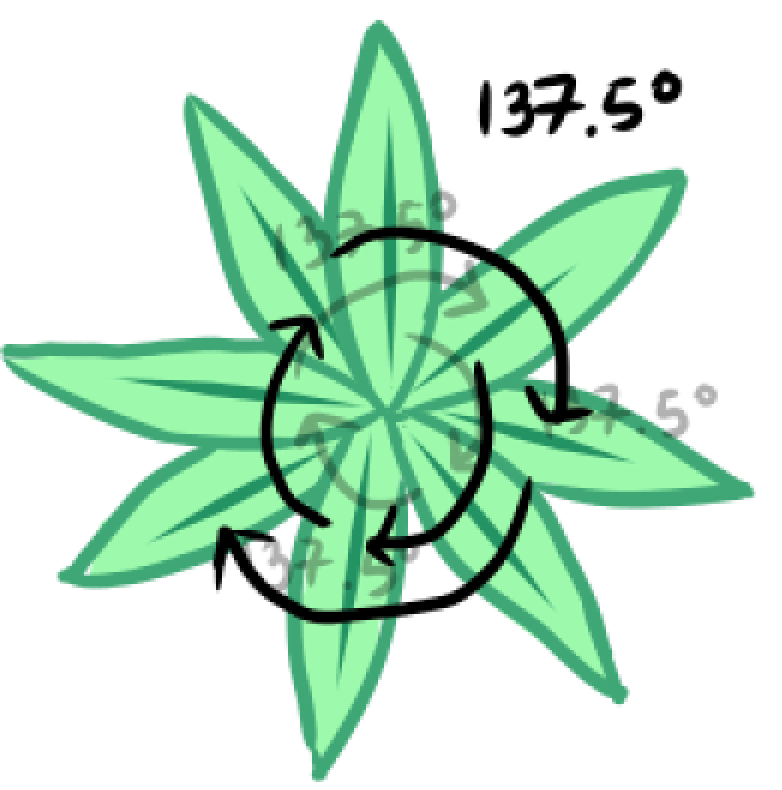
This particular example was based on leaves, but this kind of asymmetric growth happens in many other parts of a plant, as well as on the cellular level since plants grow new cells in spirals (adding a new cell after a turn).

When plants exhibit the golden angle in spiral growth patterns, this results in 2 spirals showing up, one going clockwise and the other going counterclockwise. The ratio of the bigger number of spirals to the smaller number will be one that approximates ϕ (1.618…), just like how the ratio of 2 successive Fibonacci numbers approximates ϕ as the numbers increase. When looking back at the spirals of this sunflower from before, we’ll see that the spirals correspond to 2 successive Fibonacci numbers whose ratio approximates ϕ.

34/21=1.619047

Phyllotaxis

Mathematical models and simulations have shown that patterns such as these spirals can emerge if the plant organs are made at regular intervals, but plants are not sentient beings, so how would they know how to grow? Though there is still much research to be done on their biological mechanisms, the answer may lie in the plant hormone auxin, which is responsible for stem elongation and phyllotaxis, the arrangement of leaves on a stem. Current research shows that when cells detect large amounts of auxin in nearby cells, they transport more auxin towards the cell, creating a hotspot where a new leaf grows. The creation of an auxin hotspot lowers auxin levels in the surrounding area, so new hotspots can only be formed from a certain distance away; causing leaves to be spaced out regularly to form a complex spiral pattern.

A Universal Rule?

As efficient and complex as plants’ spiral patterns are, not every leaf arrangement or pinecone displays Fibonacci numbers. After all, plants don’t always grow straight up and the sun isn’t always directly overhead. Some plants display Lucas numbers instead, a sequence similar to the Fibonacci sequence, where the next number is the sum of the two numbers before it (2, 1, 3, 4, 7, 11, 18, etc.) The difference is that the first two terms are 2 and 1, rather than 0 and 1. Despite the efficiency of the golden angle, other leaf arrangements other than the spiral also exist, such as an opposite arrangement where leaves are 180° apart. We still don’t completely know about how plant organs grow into intricate patterns on the molecular level, but one thing we’re sure of is how complex spirals in nature and a simple number sequence demonstrate the interconnectedness of math and biology.

Questions

1. What role does auxin play in plant growth?

Auxins are a class of plant hormones that regulate growth by stimulating the elongation of cells in stems. The concentration of auxin in different parts of a plant is crucial to plant development, as patterns of auxin concentration guide the growth of cells in certain areas. The spiral arrangement and presence of Fibonacci numbers in plants is hypothesized to be due to auxin hotspots that cause leaves to grow as far away from each other as possible, leading to the golden angle.

2. Why do many plants sprout new leaves at an angle of 137.5°?

By sprouting new leaves at an angle of 137.5°, also known as the golden angle, plants are able to maximize the amount of exposure to sunlight. The golden angle allows each leaf to never fully overlap with any leaf below it, so each one is able to receive sunlight. However, this rule is not completely universal; due to the many factors at play in nature, simplifying plant growth to just “maximize exposure to sunlight” is not completely accurate (e.g. the sun does not directly shine above plants at all times). This means that there are other types of phyllotaxis in plants, such as opposite, alternate, and whorled.